DSA

Introduction

· Algorithms simulation: https://www.w3schools.com/dsa/index.php

· Data Structure interview question: https://www.simplilearn.com/data-structure-interview-questions-and-answers-article

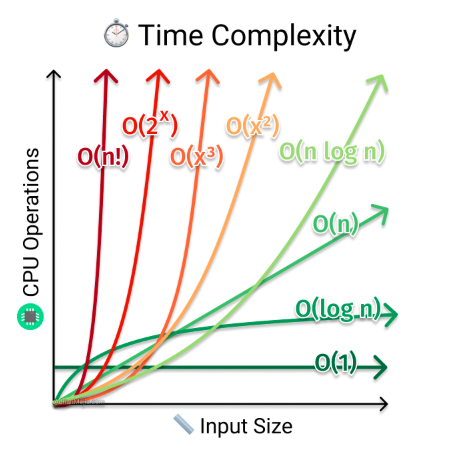
Time Complexity

· O(1) - Constant time complexity: The algorithm’s running time does not depend on the input size.

· O(log n) - Logarithmic time complexity: The running time grows logarithmically with the input size.

· O(n) - Linear time complexity: The running time grows linearly with the input size.

· O(n log n) - Linearithmic time complexity: Common in efficient sorting algorithms like merge sort and heap sort.

· O(n^2) - Quadratic time complexity: The running time is proportional to the square of the input size.

· O(2^n) - Exponential time complexity: The running time grows exponentially with the input size.

Search

·         Linear Search:

Time Complexity: O(n)

·         Binary Search:

Time Complexity: O(log n)

Sort

·         Selection Sort:

Time Complexity: O(n^2)

·         Bubble Sort:

Time Complexity: O(n^2)

·         Insertion Sort:

Time Complexity: O(n^2)

·         Merge Sort:

Time Complexity: O(n log n)

·         Quick Sort:****:

Average Time Complexity: O(n log n)

Worst-case Time Complexity: O(n^2)

Stack

A stack is a data structure that follows the Last In, First Out (LIFO) principle, where the last element added is the first one to be removed, and it is used for managing function calls, expression evaluation, and tracking state in algorithms.

We can use backtracking in algorithms like Prim’s and Kruskal’s when exploring paths. If we finish visiting a path and want to backtrack to explore other options or restart, backtracking helps us go back in the exploration process. That’s why we use backtracking in these algorithms.

Queue

A queue is a data structure that follows the First In, First Out (FIFO) principle, where the first element added is the first one to be removed, and it is used for managing data in a sequential order, such as in task scheduling, print spooling, and breadth-first search algorithms.

·         Linear Queue:

The standard queue where elements are added at the rear (enqueue) and removed from the front (dequeue).

·         Circular Queue:

Similar to a linear queue, but the rear and front pointers wrap around, creating a circular structure. This helps in efficient space utilization and prevents overflow or underflow conditions.

·         Priority Queue:

Elements in a priority queue have associated priorities, and elements with higher priorities are served before those with lower priorities. Priority queues can be implemented using various data structures, such as heaps.

·         Double-ended Queue (Deque):

A queue that allows insertion and deletion at both the front and rear ends. It combines the features of a queue and a stack.

·         Blocking Queue:

A queue that blocks or waits when trying to dequeue from an empty queue or enqueue to a full queue. It is often used in concurrent programming and multithreading.

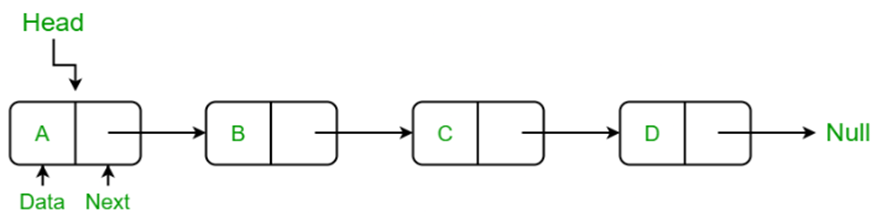
Linked List

A linked list is a linear data structure where elements are stored in nodes, each pointing to the next one, and it is used for dynamic memory allocation, efficient insertion and deletion, and building other data structures like stacks and queues.

Real world scenario of uses of this:

·         Dynamic Memory Allocation:

Linked lists are commonly used in dynamic memory allocation scenarios, such as in programming languages like C or C++. When the size of data is not known in advance, linked lists provide a flexible way to allocate memory as needed, unlike arrays that require a fixed size.

·         Task Management in Operating Systems:

Operating systems often use linked lists for managing tasks and processes. Each task is represented as a node in the linked list, and the operating system can efficiently add, remove, or reorder tasks by manipulating the pointers between nodes. This dynamic structure is well-suited for handling various task scheduling scenarios.

The main types of linked lists include:

·         Singly Linked List:

Each node contains data and a reference (pointer) to the next node in the sequence.

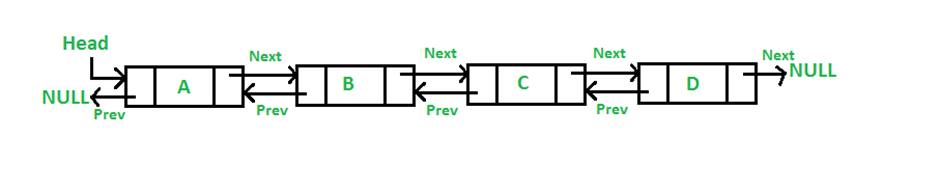
·         Doubly Linked List:

Each node contains data and references to both the next and the previous nodes, allowing for traversal in both directions.

·         Circular Linked List:

Similar to a singly linked list, but the last node points back to the first node, forming a circular structure.

·         Doubly Circular Linked List:

Combines features of a doubly linked list and a circular linked list, with nodes having references to both the next and previous nodes and the last node pointing back to the first.

Singly linked list image:

Example of singly linked list using C#:

class Node
{
    public int Data;
    public Node Next;
 
    public Node(int data)
    {
        Data = data;
        Next = null;
    }
}
 
class LinkedList
{
    private Node head;
 
    public LinkedList()
    {
        head = null;
    }
 
    public void InsertAtEnd(int data)
    {
        Node newNode = new Node(data);
 
        if (head == null)
        {
            head = newNode;
        }
        else
        {
            Node current = head;
 
            while (current.Next != null)
            {
                current = current.Next;
            }
            current.Next = newNode;
        }
    }
 
    public void Display()
    {
        Node current = head;
        while (current != null)
        {
            Console.Write(current.Data + " ");
            current = current.Next;
        }
    }
}
 
class Program
{
    static void Main()
    {
        LinkedList linkedList = new LinkedList();
        linkedList.InsertAtEnd(1);
        linkedList.InsertAtEnd(2);
        linkedList.InsertAtEnd(3);
        linkedList.InsertAtEnd(4);
        Console.WriteLine("Linked List elements:");
        linkedList.Display();
    }
}

Doubly linked list image:

Feature	Singly Linked List	Doubly Linked List
Node Structure	Contains data and a next pointer.	Contains data, next, and prev pointers.
Direction of Traversal	Forward only (next).	Forward and backward (next and prev).
Memory Overhead	Lower memory overhead per node.	Higher memory overhead due to an extra pointer per node.
Insertion/Deletion	Faster for insertions and deletions at the beginning and in the middle.	Slightly slower due to updating both next and prev pointers.
Implementation Complexity	Generally simpler to implement.	Slightly more complex due to handling prev pointers.
Memory Usage	More memory-efficient.	Requires more memory due to additional pointers.

Tree

·         Binary tree

A binary tree is a hierarchical data structure composed of nodes, where each node has at most two children, referred to as the left child and the right child. The topmost node in the tree is called the root node. Binary trees are commonly used for representing hierarchical structures like binary search trees, expression trees, and directory structures.

Pre order, In order, Post order traversal

Some Algorithms

·         BFS

·         DFS

·         Prims

·         Kruskal

·         Diskjstra

·         Bellman Ford

·         Knapsack

·         Greedy Method